| Главная » Статьи » Мои статьи |
Булева алгебра для Ladder Logic
Коммутативностьa or b = b or a
a and b = b and a
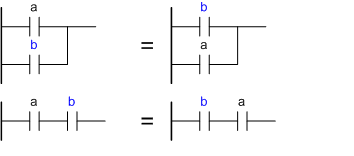 Первое равенство -
Если для срабатывания системы требуется или нажатие кнопки a или нажатие кнопки b,
то можно считать, что требуется или нажатие кнопки b или нажатие кнопки a.
Второе равенство -
Если для срабатывания системы требуется одновременное нажатие кнопок a и b,
то можно считать, что требуется одновременное нажатие кнопкок b и a.
Ассоциативностьa or (b or c) = (a or b) or c
a and (b and c) = (a and b) and c
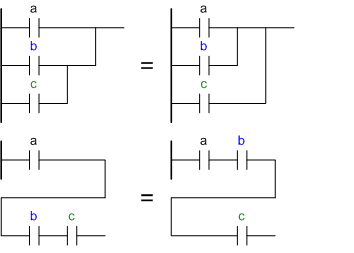 Аналогично коммутативности, только с тремя кнопками, поделенными на две группы.
Дистрибутивностьa or (b and c) = (a or b) and (a or c)
a and (b or c) = (a and b) or (a and c)
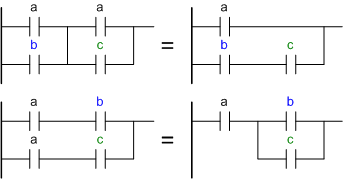 Первое равенство -
Если для срабатывания системы требуется или нажатие кнопки a или нажатие кнопки b, одновременно с которыми требуется нажатие кнопки a или нажатие кнопки с, то можно считать, что требуется или нажатие кнопки a или нажатие кнопки b одновременно с кнопкой c. Второе равенство - Если для срабатывания системы требуется одновременное нажатие кнопок a и b либо одновременное нажатие кнопок a и c, то можно считать, что требуется одновременное нажатие кнопкок a и одной из двух - b или c. Комплементностьa or not(a) = 1
a and not(a) = 0
 Первое равенство -
Если для срабатывания системы требуется нажатие кнопки a и одновременно отсутствие нажатия кнопки a, то можно считать, что система никогда не сработает. Второе равенство - Если для срабатывания системы требуется нажатие кнопки a или отсутствие нажатия кнопки a, то можно считать, что система будет работать постоянно. Законы де Морганаnot(a or b) = not(a) and not(b)
not(a and b) = not(a) or not(b)
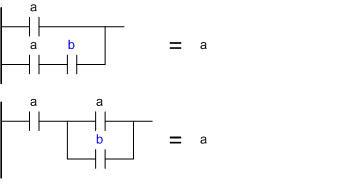
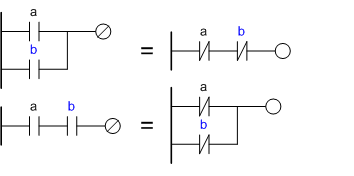 Законы поглощенияa or (a and b) = a
a and (a or b) = a
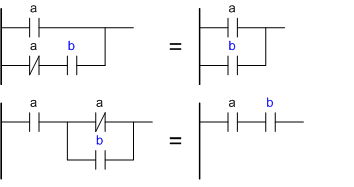
 Закон Блейка-Порецкогоa or (not(a) and b) = a or b
a and (not(a) or b) = a and b
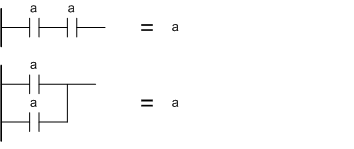
 Идемпотентностьa or a = a
a and a = a
 Инволютивность отрицанияnot(not(a)) = a
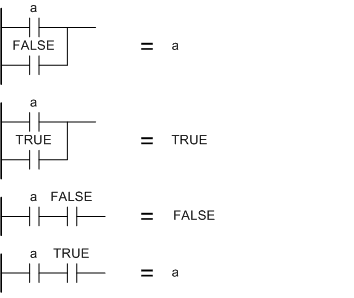
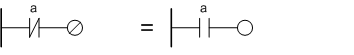 Свойства константa or 0 = a
a and 0 = 0
a or 1 = 1
a and 1 = a
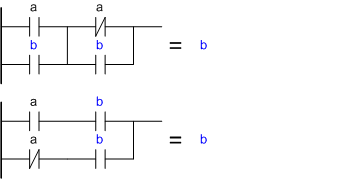
 Склеивание(a or b) and (not(a) or b) = b
(a and b) or (not(a) and b) = b
 | |
| Просмотров: 2775 | Теги: | Рейтинг: 0.0/0 |
| Всего комментариев: 0 | |